
1. 某单位共有A、B、C三个部门,其中A部门与B部门员工之和为30人,A部门与C部门员工之和为40人,B部门与C部门员工之和为50人,则B部门员工人数为:
A.20
B.30
C.40
D.50
2. 甲、乙、丙三人绕圆形跑道赛跑。甲跑完一圈要1分钟,乙跑完一圈要1分30秒,丙跑完一圈要1分15秒。现在三个人同时同向从同一地点出发,则( )分钟后三人又在出发地相遇。
A.3
B.9
C.10
D.15
3. A班50名同学参加某次考试,共有5道题,每题20分,答对得满分,答错不得分,有35人答对第一题,40人答对第二题,42人答对第三题,37人答对第四题,45人答对第五题,则该次考试至少有( )人达到或超过60分。
A.16
B.20
C.33
D.35
4. 一个三位数,百位数字为9,十位数字为a,个位数字为b,且9、a、b为三条边的长可以构成一个等腰(含等边)三角形。则这样的三位数有( )个。
A.22
B.20
C.21
D.23
5. 一项工程由A与B两人合作完成,若由A、B独立完成,则分别需要18天和27天。现规定按如下方案实施工程,先由A做一天,B接着做两天,再由A做一天,B接着做两天……如此反复,直到工程全部完成为止。则B实际做的天数为:
A.13
B.14
C.15
D.16
6. 某鲜花店在情人节当天中午决定加大促销力度,对一款鲜花进行降价处理,现已知该款鲜花成本价每束50元,标价每束80元时销量20束。如果每降价5元,则销量增加10束,那么降价多少元,收益最大?
A.5
B.10
C.15
D.20
答案解析...请翻下一页哦~
| 2024云南省事业单位备考推荐 | |
| 2024下半年云南事业单位公告预约 | 云南事业单位职位在线查询 |
| 2024云南事业单位全省岗位表下载 | 云南事业单位考试专题信息网 |
| 2024云南事业单位联考图书4本套 | 2024云南事业单位D类4本套 |
| 2024云南事业单位联考必做题库 | 2024事业单位D类必做题库 |

1.【答案】A
【解析】第一步,本题考查基础应用题,用方程法解题。
第二步,设A、B、C三个部门人数分别为x、y、z,由题意可得:x+y=30①、x+z=40②、y+z=50③,联立方程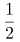 (①+②+③)-②,可得y=20(人)。
(①+②+③)-②,可得y=20(人)。
因此,选择A选项。
2.【答案】D
【解析】第一步,本题考查约数倍数问题。
第二步,甲跑完一圈要1分钟,乙跑完一圈要1分30秒,丙跑完一圈要1分15秒,即甲、乙、丙用的时间分别为60秒、90秒、75秒,下一次在出发地相遇时间应为60秒、90秒、75秒的最小公倍数900秒,即15分钟。
因此,选择D选项。
3.【答案】C
【解析】解法一:
第一步,本题考查最值问题,属于其他最值构造。
第二步,每题20分,让达到或超过60分的人数尽可能少,也就是答对3题及以上的人数要尽可能少,反向构造答错3题及以上的人数尽可能多。因5道题分别答对的人数为:35、40、42、37、45,则5道题分别答错的人数为:15、10、8、13、5,即答错的总人次为15+10+8+13+5=51,要想答错3题及以上的人数尽可能多,则让每个人答错的题尽可能少,即每人均答错3题,故答错3题及以上的人数最多有 =17,答对3题及以上的人数最少有50-17=33。
=17,答对3题及以上的人数最少有50-17=33。
因此,选择C选项。
解法二:
第一步,本题考查最值问题,属于其他最值构造。
第二步,因5道题分别答对的人数为:35、40、42、37、45,故50名同学共答对35+40+42+37+45=199(道)题。每题20分,如果要达到或超过60分的人数尽可能少,即答对3题以及上的人数要尽可能少,则先让50名同学先每人答对2题,还剩下199-50×2=99(道)题。要让达到或超过60分“至少”,则让满分的人尽可能多,故最多有 =33(人)满分,
=33(人)满分,
4.【答案】C
【解析】第一步,本题考查几何问题,属于几何特殊性质类。
第二步,当a=9时,b>9-a,则b取值为1、2、3、……、9,共9种;当b=9且a≠9时,a>9-b,则a取值为1、2、3、……、8,共8种;当a=b≠9时,a+b>9,取值为5、6、7、8,共4种,这样的三位数有9+8+4=21(个)。
因此,选择C选项。
【拓展】三角形:任意两边之和大于第三边,任意两边之差小于第三边。
5.【答案】C
【解析】第一步,本题考查工程问题,属于时间类,用赋值法解题。
第二步,根据题意赋工作总量为54(18和27的公倍数),则A的效率为3,B的效率为2。先由A一天,B接着做两天,这三天的工作量为7,每三天为一个周期,则54÷7=7…5,即完成7个周期后,还剩5个工作量,每个周期B工作2天,因此B干了7×2=14(天)。剩下的5个工作量,先由A干1天之后还剩2个工作量,则还需要B再干1天,因此B总共干了14+1=15(天)。
因此,选择C选项。
6.【答案】B
【解析】第一步,本题考查经济利润问题,属于最值优化类,用方程法解题。
第二步,总利润=单件利润×总销量,设降价n次,一次降价5元,n次降价5n元,则单件利润为(80-5n-50)元;降价一次,销量提高10束,n次销量提高10n束,则总销量为(20+10n)束。故总利润=(30-5n)×(20+10n)=2(30-5n)(10+5n),当30-5n=10+5n,n=2(次)时,总利润取最大。所以降价5×2=10(元),收益最大。
因此,选择B选项。










